Le compte est bon

Principe de l’algorithme de résolution

Vue d’ensemble

La première partie consistera à réaliser le tirage aléatoire des six plaques et du nombre N  et à mettre les valeurs des plaques dans un tableau (CompteEstBonAlgo::Calcul())

La deuxième partie consistera à rechercher la solution optimale (CompteEstBonAlgo::resoudre).
Pour cela, on partira du résultat à trouver (Valeur) ou en cas d'échec, Valeur -1, Valeur +1, Valeur -2, Valeur +2, etc…, et on cherchera à obtenir en utilisant les six plaques.

Une difficulté est de choisir une bonne représentation pour les ensembles d'entiers. On choisira la représentation qui permet le calcul le plus rapide (le type long) et on évitera toute conversion inutile.

La règle n’autorisant l’utilisation que d’une plaque à la fois une implémentation récursive de la résolution est bien adaptée à ce type de traitement. L’algorithme de recherche de solution repose sur l’application exhaustive de toutes les opérations entre toutes les combinaisons de plaques.

On effectuera donc au maximum C₆² *  4 * C₅² *  4 * C₄² *  4 * C₃² *  4 * C₂² *  4  soit  2764800 opérations arithmétiques.

En réalité, les contraintes liés aux opérations arithmétiques diminuent sensiblement le nombre d’opérations effectuées. En effet, la division est dans la plupart des cas non réalisables (une opération de moins sur les 4).

Le nombre minimum quant à lui correspond au cas ou le résultat de la première opération avec les 2 premières plaque correspond à la valeur recherchée.

L’algorithme prend les 2 premières plaques parmi les 6 et on effectue la première opération arithmétique. Si le résultat de l’opération est acceptable (résultat entier pour une division par exemple) on reconstitue un tableau de plaques avec ce résultat auquel on ajoute pour les indices suivants les 4 autres plaques restantes. Chaque changement d’opération fait suite à l’échec de tous les calculs effectués à partir des plaques restantes.

Vue détaillée :

On dispose de 6 plaques {p₁,p₂,p₃,p₄,p₅,p₆}, on choisit 2 plaques parmi ces 6 plaques :
Il y a donc = 6x5/2 = 15 combinaisons :
{(p₁,p₂),(p₁,p₃),(p₁,p₄),(p₁,p₅),(p₁,p₆),(p₂,p₃),(p₂,p₄),(p₂,p₅),(p₂,p₆),(p₃,p₄),(p₃,p₅),(p₃,p₆),(p₄,p₅),(p₄,p₆),(p₅,p₆)}

Pour chacun des couples (p_i,p_j), on dispose des 4 opérations arithmétiques.
La soustraction et la division n'étant pas commutative, il faut aussi penser à l'inverse :
p_i - p_j et aussi p_j - p_i
p_i / p_j et aussi p_j / p_i

Remarque :

p₁ + p₂ = p₂ + p₁ (commutativité de l'addition)
p₁ x p₂ = p₂ x p₁ (commutativité de la multiplication)

En y regardant de plus près, seules les valeurs positives nous intéressent :
Hors si p₁ - p₂ > 0 alors p₂ - p₁ < 0
Et si p₁ - p₂ > 0 alors p₁> p₂ et p₂ / p₁ n'existe pas (valeur non entière).

On peut donc tester le couple (p_i,p_j) et faire ensuite la soustraction qui est positive :
p_i - p_j ou p_j - p_i.
Si la soustraction est nulle, on peut éliminer le calcul, la valeur nulle ne pouvant nous aider dans la recherche de solutions.

On fait de même la division p_i / p_j ou p_j / p_i suivant le test.
Ce qui ramène le couple (p_i,p_j) à quatre opérations arithmétiques (la multiplication et surtout la division étant les plus coûteuses).
Si p_i ou p_j dans la multiplication (ou la division) est de valeur 1, alors p_i x p_j = p_i ou p_j (p_i / p_j = p_i si p_j = 1) et donc ces opérations ne font pas avancer le calcul et la recherche de solutions :
On peut donc éliminer ces cas également.
Si la division n'existe pas dans N, ce qui est très fréquent, on évite une opération de plus, ce qui donne en tout moins de 4 opérations en moyenne par couple (p_i,p_j).

On a donc 15 couples (p_i,p_j), et au plus 4 opérations pour chacun de ces couples, soit au plus 60 opérations pour les 2 premières plaques.

Supposons l'opération p_i + p_j :
La valeur calculée peut être considéré comme une nouvelle plaque.

On se retrouve alors avec le même problème mais avec 5 plaques et non plus avec 6 (2 plaques remplacées par le résultat de l'opération entre ces 2 plaques), il y a donc 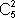= 5x4/2 = 10 combinaisons.
Si par exemple p₁ et p₂ étaient les 2 premières plaques utilisées et si p₁ devenait le résultat de la première opération de p₁ et p₂, on a ces 10 combinaisons :
{(p₁,p₃),(p₁,p₄),(p₁,p₅),(p₁,p₆),(p₃,p₄),(p₃,p₅),(p₃,p₆),(p₄,p₅),(p₄,p₆),(p₅,p₆)}

On fait le même raisonnement avec 4 plaques, 3 plaques, puis 2 plaques.

Dès qu'il ne reste plus qu'une seule plaque on dépile.

A chaque niveau de récursivité, on vérifie si le résultat de l'opération faite au niveau de récursivité précédent n'est pas le résultat qu'on cherche (simple test sur la nouvelle plaque issue des 2 anciennes : si p₁ est toujours le résultat de l'opération précédente, on teste simplement si p₁ est le résultat qu'on cherche).

Graphes de l'algorithme :

Ces graphes illustrent le fonctionnement de l'algorithme récursif :